地理信息系统中的常用坐标系
- 地理坐标系 (Geographic Coordinate System, GCS)
- 投影坐标系 (Projected Coordinate System, PCS)
- 垂直坐标系
- 三维笛卡尔坐标系
- 坐标系转换
- Reference
地理坐标系 (Geographic Coordinate System, GCS)
介绍
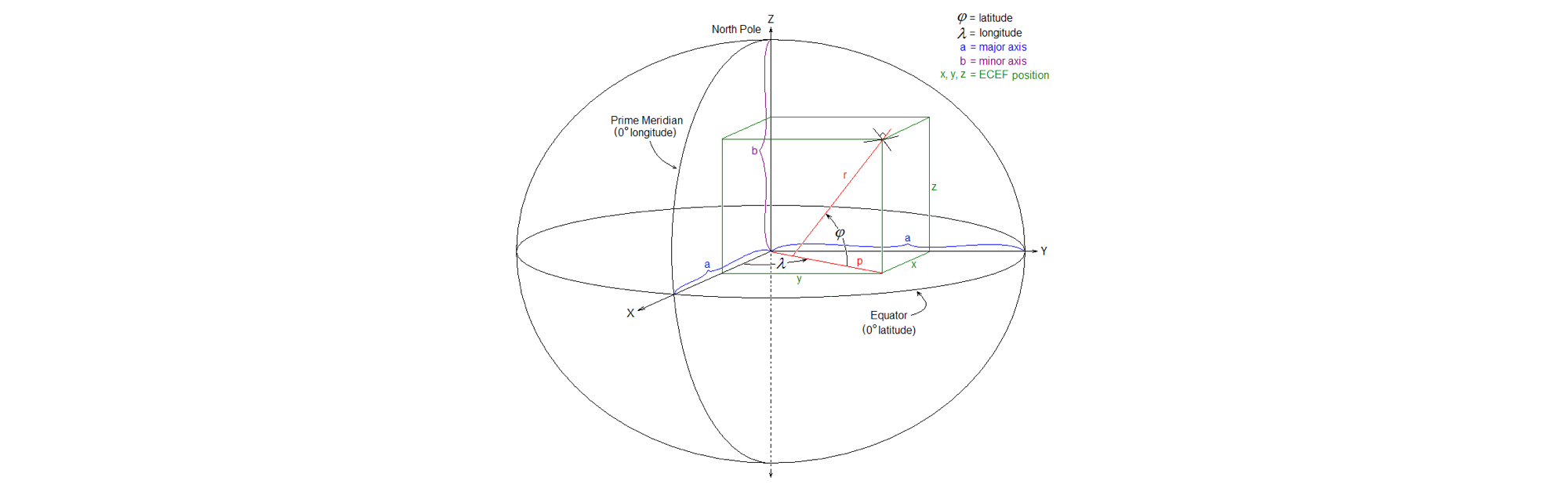
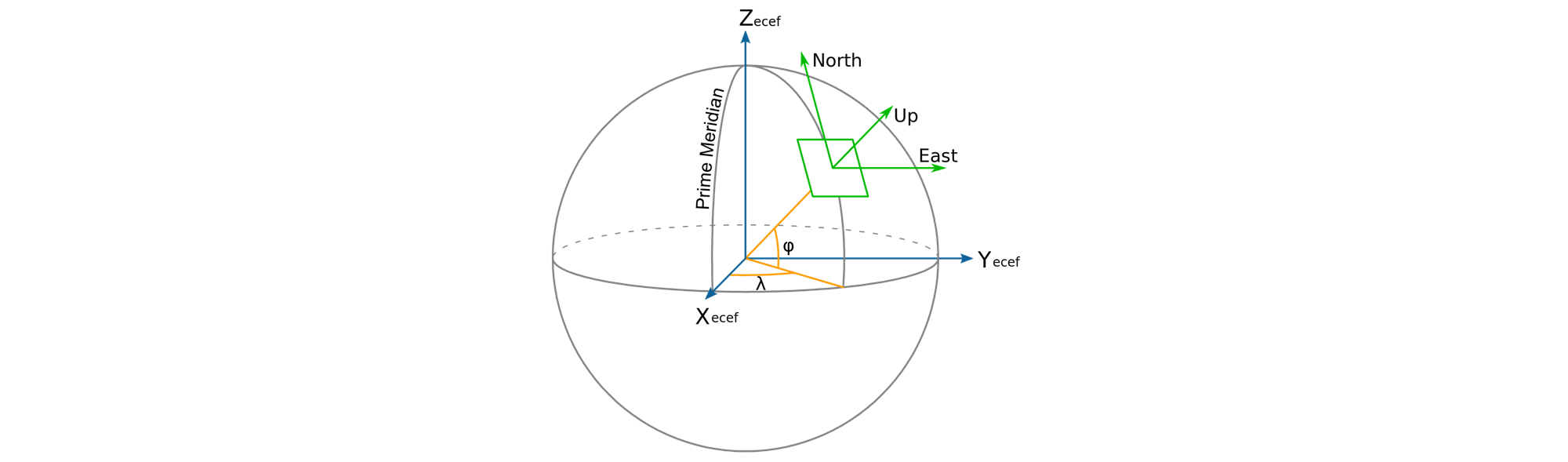
地理坐标系是在三维球面上用经度和纬度值定义的坐标系,它描述了地球球面上某点的测量角。坐标系以赤道和本初子午线的交点为原点,以指向北极点的极轴为Z轴,以指向赤道和本初子午线的交点为X轴,以指向赤道和东经90度经线的交点为Y轴。纬度的范围是-90~90度,经度的范围是-180~180度。注意,地表某点的纬度等于该点的法线和Z轴的夹角,如图1所示。
基准面
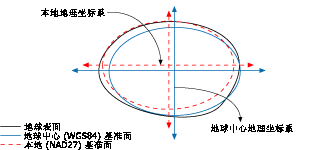
由于地球表面复杂的地理结构,地球并不是一个严格的球体,也不是严格的椭球体。因此在定义地理坐标系时需要用一个标准的椭球体去拟合地球表面的几何形状,由此产生很多不同的基准面的定义。
- 地心基准面。地心基准面以地球的质心为球心。例如使用最广泛的 WGS 1984,是在世界范围内进行定位测量的框架。
- 区域基准面。为了用椭球体拟合测绘的特定区域,区域基准面应运而生,例如 NAD 1927 旨在尽可能与北美洲吻合,而 ED 1950 是为欧洲而构建。如图1所示,区域基准面的旋转椭球体的球心一般与地心存在一定偏移。
- 基于不同的基准面定义的不同的地理坐标系详见link。
投影坐标系 (Projected Coordinate System, PCS)
介绍
众所周知,我们地球的表面是一个球面或椭球面,因为球面或椭球面无法无缝展开成平面,所以就需要通过投影的方式,将地球表面投射到可展开曲面(称为投影曲面)上生成二维平面地图。常用的投影曲面包括圆锥、圆柱或一个单纯的平面。投影时,可假设有一个光源(例如放置在地心),光线穿过地球表面某一点A,落在投影曲面上的位置即为点A的坐标。
根据投影曲面和“光源”位置的不同,我们将地图投影主要分为圆锥投影、圆柱投影、平面投影。不同的投影方式定义了不同的投影坐标系。
圆锥投影
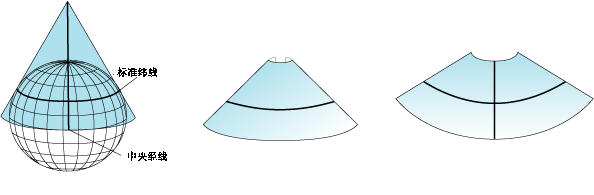
顾名思义,圆锥投影就是投影曲面为圆锥的投影。常见地,如果圆锥的轴与极轴重合,圆锥曲面恰好与地球表面相切于一条纬线,则这条纬线称为标准纬线,因为它的长度在投影后未经过任何拉伸或变形。随着距离标准纬线越远,变形就越明显。如果圆锥曲面与地球表面相割,则两条割线都是标准纬线。通常,割线投影的整体变形程度小于切线投影。
圆柱投影
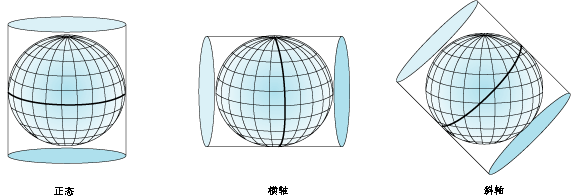
圆柱投影使用圆柱作为投影平面。和圆锥投影类似,圆柱投影分为相切和相割两种情况。墨卡托投影是最常用的圆柱投影之一,并且通常以赤道为切线。这种投影方式产生成90度的经纬网格。经线等间距排列,而纬线间的间距越靠近极点越大。如下图所示,是通用横轴墨卡托投影(UTM)的示意图:
平面投影

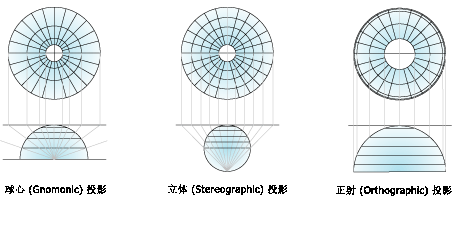
平面投影也称为方位投影或天顶投影。它将地图数据投影到与地球相切(亦有可能相割)的平面上。切点可能位于极点、赤道上或任意一点。其中最常见地,当切点位于极点时,就是极方位投影,最常用于绘制两极地区的地图。根据透视点(即“光源”)的位置来分类,分为球心投影(透视点在地心)、立体投影(透视点在两极之间)、正射投影(光源在无穷远处)。
投影参数
以上的投影方式交代了生成二维地图投影的过程。不同的投影方式会产生不同的坐标系统。另外,因为投影变换过程中会产生形变,不同地区为减小该地区的形变会调整投影曲面的位置,由此产生更加繁多的投影坐标系统(详见link)。 在实际使用中,还需要在投影地图中定义坐标轴,包括原点位置,X轴Y轴的方向,比例尺等。此外,因为投影坐标系只提供X-Y的坐标,如需要测量高度,还需要另外的高程测量以提供Z值。
垂直坐标系
上面讲到的地理坐标系和投影坐标系只定义了目标点在二维表面的位置,缺少了高度的测量。垂直坐标系通过定义高程基准提供对空间中任意一点的高度测量。常用的高程基准有两种。
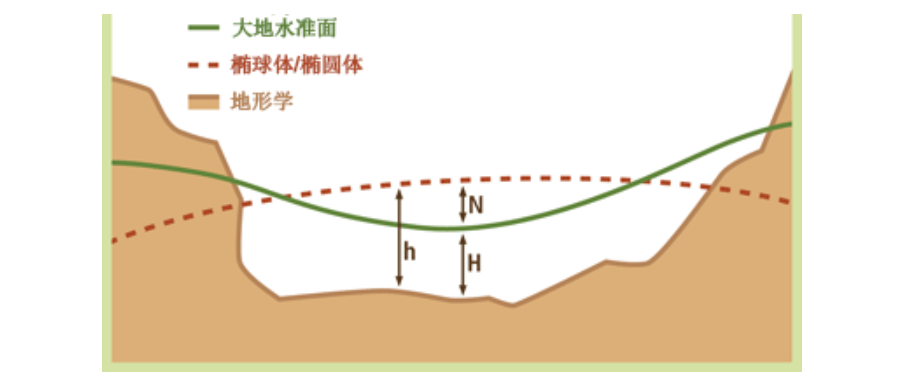
一种是数学基准,使用地理坐标系中的椭球体基准面作为高度为0的曲面。因为它是一种理想的数学定义,该基准所测量的高度并不能反映地球表面高低起伏的地理结构,甚至造成“水往高处流”的情形。
另一种是分析基准,使用大地水准面作为高程基准(如1985年国家高程基准)。大地水准面是假设海洋受重力影响在地球表面生成的静态曲面。由于地球上各个地方的重力的不同,该曲面的形状极不规则,但其高度负方向与重力方向一致,不会出现“水往高处流”的情形。简单来说,如果A点的水能往B处流,那A比B高。示意图如下所示。
各种垂直坐标系详见link
三维笛卡尔坐标系
三维笛卡尔坐标系是用三维笛卡尔坐标描述某点的坐标系。常用的包括地心地固坐标系(ECEF)和站心地平直角坐标系(ENU)。
地心地固坐标系 (ECEF)
地心地固坐标系(Earth Center Earth Fixed, ECEF)和图1地理坐标系共用相同的坐标原点和坐标轴,但是使用笛卡尔坐标而非角度来描述点的位置。
站心地平直角坐标系 (ENU)
站心地平直角坐标系(East North Up, ENU)是定义在地表正切平面的局部坐标系。如下图所示,它以站心点的纬线方向(指东)为X轴,以站心点的经线方向(指北)为Y轴,以站心点的法线(指上)为Z轴。
坐标系转换
地理坐标系到地心地固坐标系 (GCS to ECEF)
地理坐标系和地心地固坐标系共用了同一套坐标轴。上图中,椭圆表示了地球的横截面,纵轴为Z轴,横轴为X-Y平面。假设地球的赤道半径为\(a\),极轴半径为\(b\)。地表上空\(R\)点的地理坐标为:纬度\(\phi\),经度\(\lambda\),海拔\(h\)。\(P\)点为发现\(RQ\)与椭球面的交点。首先,可计算得
\[\begin{split} PQ &= N(\phi)=\frac{a^2}{\sqrt{a^2 cos\phi^2 + b^2 sin \phi^2}} = \frac{a}{\sqrt{1- e^2 sin \phi^2}}, \\ IQ &= e^2 N(\phi), \\ PI &= \frac{b^2}{a^2} N(\phi).\end{split}\]此处, \(e^2 = 1 - \frac{b^2}{a^2}\)。那么\(R\)点的ECEF坐标可以计算为
\[\begin{split} X &= (N(\phi) + h)cos\phi cos\lambda ,\\ Y &= (N(\phi) + h)cos\phi sin\lambda,\\ Z &= (\frac{b^2}{a^2} N(\phi) + h) sin \phi. \end{split}\]地心地固坐标系到地理坐标系 (ECEF to GCS)
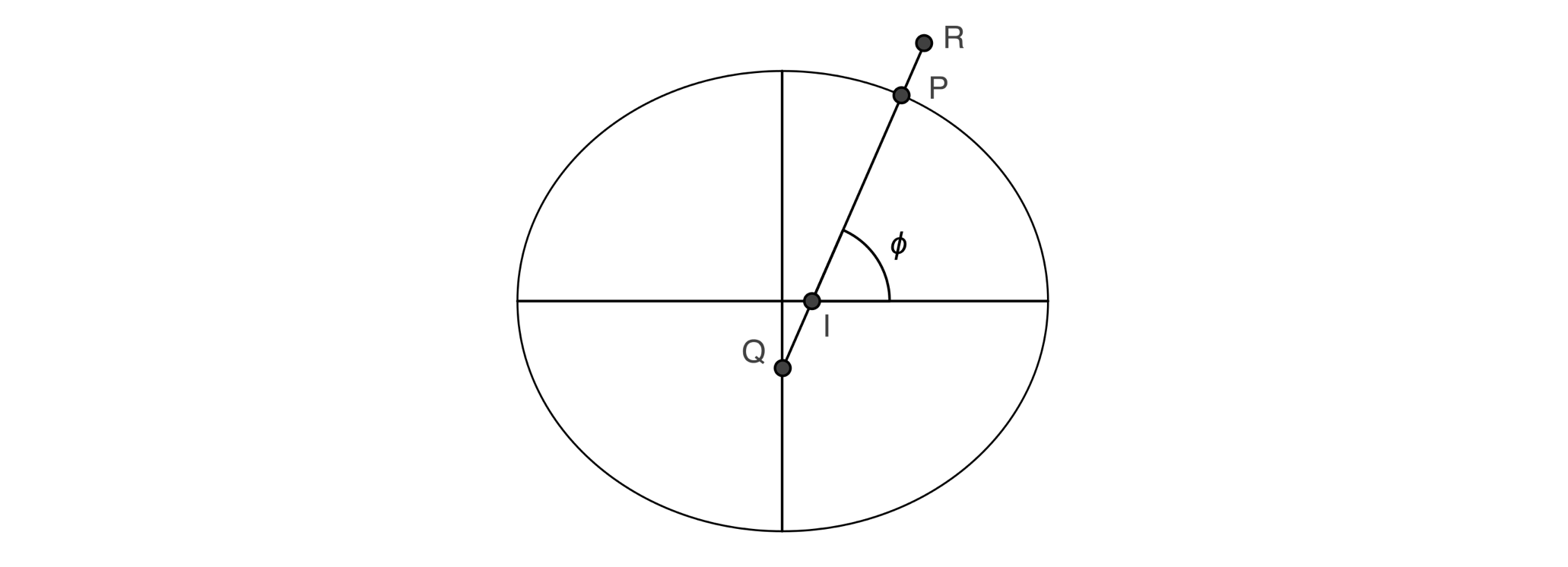
在这一步的坐标系转换中,经度的计算比较简单,即\(tan \lambda = \frac{Y}{X}\)。纬度的计算较为复杂,如下图所示(摘自wikipedia)。

ECEF to ENU
由于ENU坐标系定义在局部坐标系下,所以转换前需要知道ENU局部坐标系的原点的ECEF坐标\((X_r, Y_r, Z_r)\),以及原点的经度\(\phi\)和纬度\(\lambda\)。计算式为:
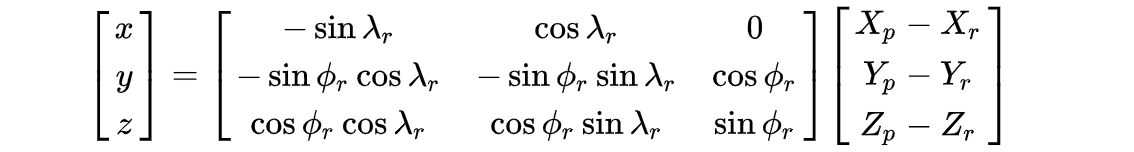
ENU to ECEF
计算式如下。此矩阵与上面的矩阵互为逆矩阵。
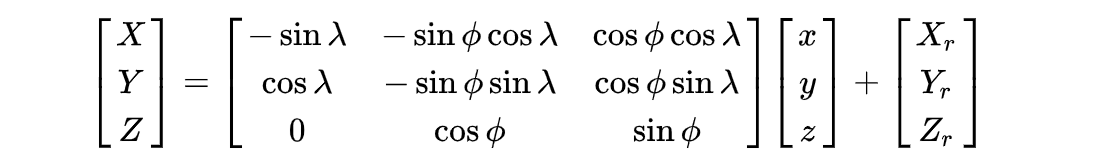
GCS to ENU
GCS和ENU之间的坐标系转换通过先转换为ECEF实现。
涉及投影坐标系的转换
投影坐标系之间的转换一般通过一个中间坐标系来实现,例如ECEF。
Reference
http://desktop.arcgis.com/zh-cn/arcmap/10.3/guide-books/map-projections/what-are-map-projections.htm