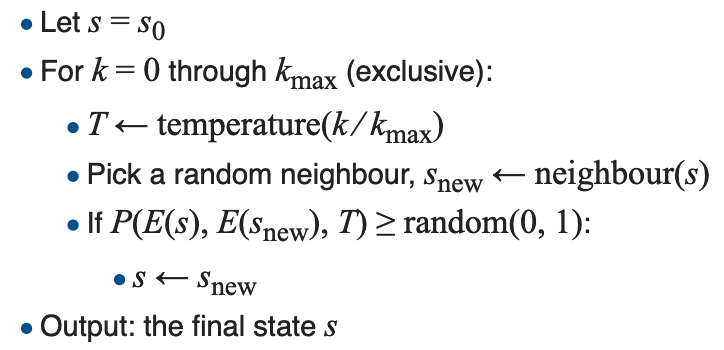Simulated Annealing

Simulated Annealing is an adaption of the Metropolis-Hastings (MH) algorithm into the field of non-convex optimization. We refer the reader to link to get to know about the MH algorithm. It is usually applied to look for the global optima inside a large parameter space where a large number of local optima occur.

Different from the greedy optimization algorithms like gradient descent, gauss-newton and LM algorithms, it always makes a move with some probability less than 1. It means the algorithm is nondeterministic. The randomness introduced allows the possibility that an uphill move can be made towards a point with larger loss (or say, energy). It is favorable to let the optimization escape from local optima and explore a larger search space.

However, the probability of making a bad (loss-increasing) move gradually decreases to zero, as the temperature \(T\) gets down with time according to some “annealing schedule”. Thus, simulated annealing will become equivalent to the greedy optimizers ultimately which identify a minima within a local neighborhood.

The pseudocode from Wikipedia writes