Overview

In this post, we are targetted at high-definition LiDAR point clouds that are ubiquitously used in autonomous driving. Typically, point clouds acquired by Terrestrial LiDAR (cf. Airborne LiDAR which typically mounted on aircrafts) sensors possess ~100k points, which are sparse actually and have large variations in density.

Applications

1. PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation

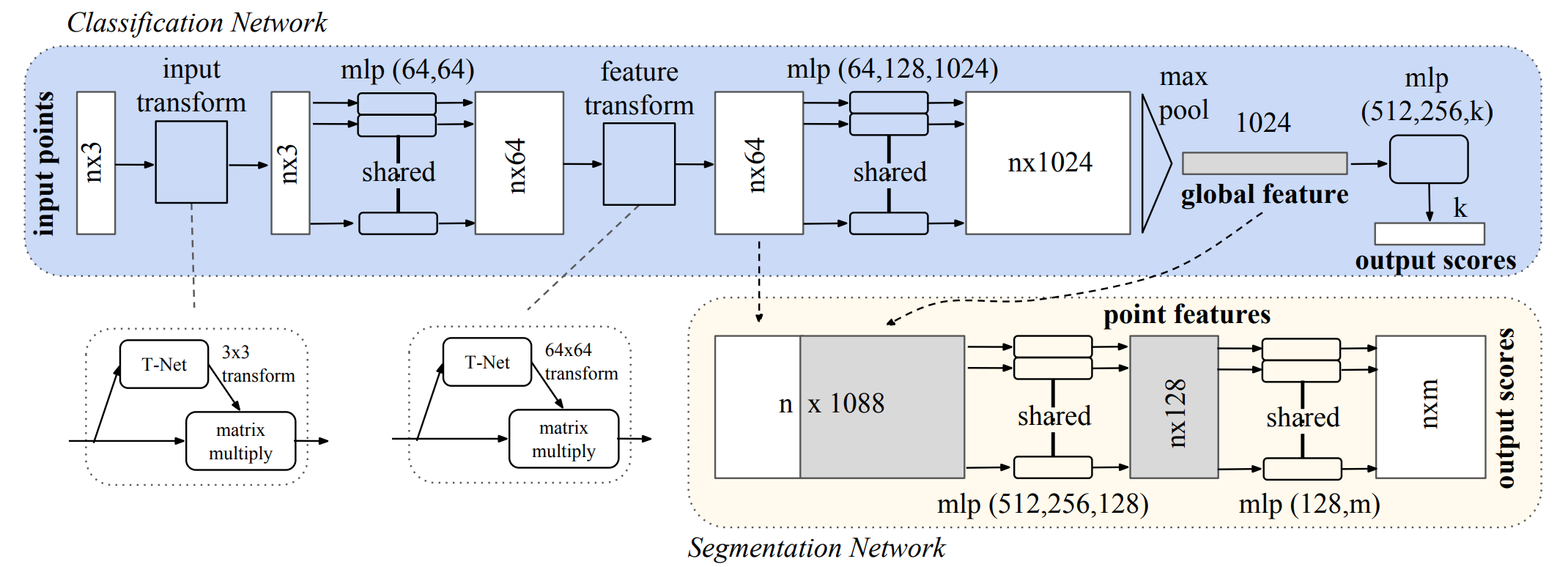
Point clouds are not ideal data format for deep learning operators due to their irregular properties and inherent variance. PointNet addresses the extraction of semantic knowledge of point clouds that is invariant to point order, point density and euclidean transformation. To conclude:

• Invariance to order – The element-wise pooling of points’ feature vectors takes care of variance to order and size of point sets. The feature network takes point set as input and gives a global signature - a K-dimensional descriptor.
• Invariance to density – Ideally the model should be able to give stable prediction, e.g., the same classification and segmentation scores, in spite of cetrain perturbation of points (contraction or expansion). The paper provides inspring definition of critical point set which is a subset of original point set but gives the same prediction as original point set. (Only the points yielding maximum reponse in any dimension contribute to final descriptor. Conversely, adding points that do not result in maximum reponses in K-dim descriptor would not affect prediction results.
• Invariance to transformation – The transformation invariance is achieved by aligning inputs to a canonical space. It use a T-net to predict a \(3\times3\) affine transformation matrix and a \(64\times64\) feature transformation matrix.

2. VoxelNet: End-to-End Learning for Point Cloud Based 3D Object Detection

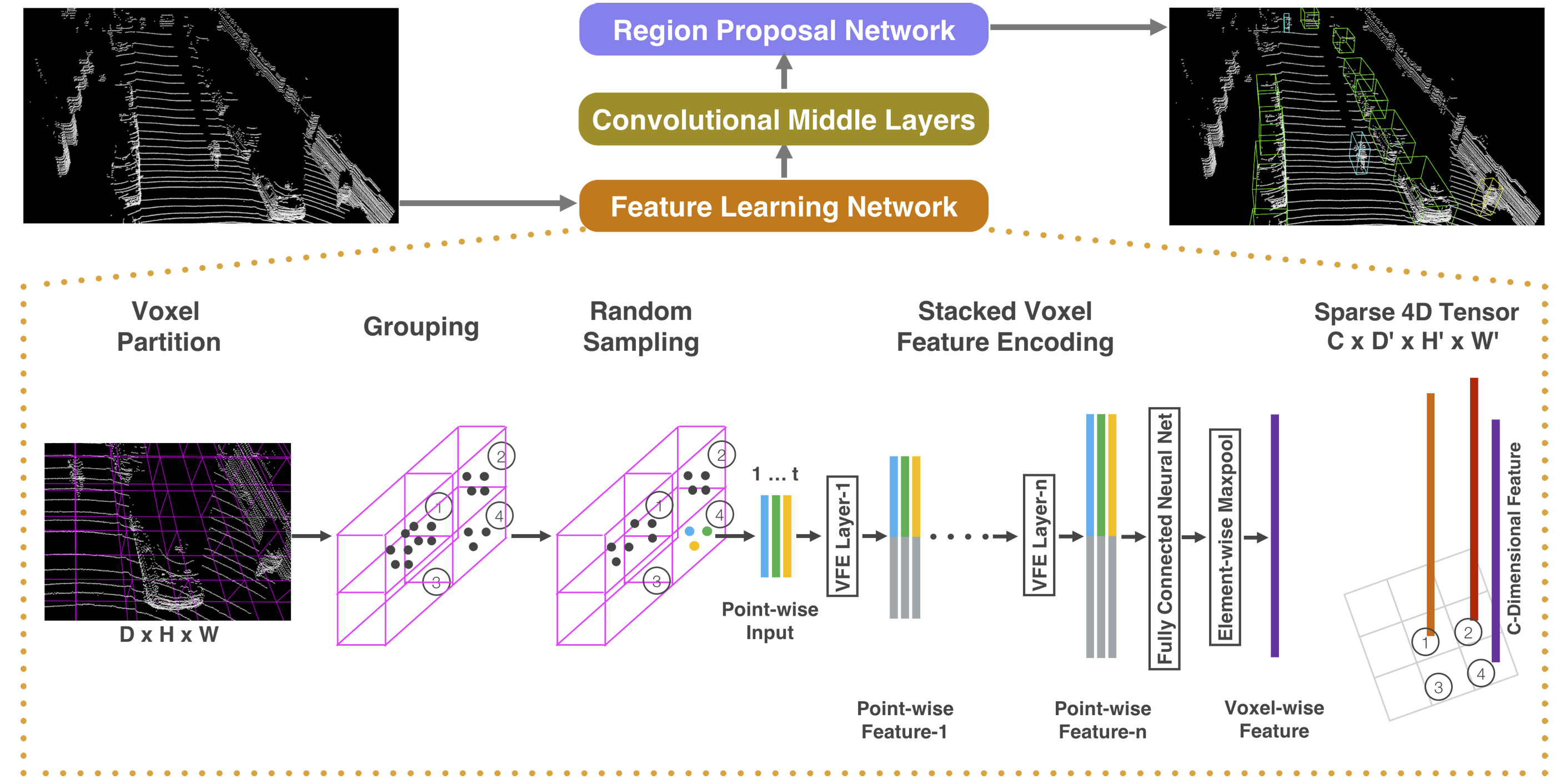
Objection detection, like cars, pedestrians and cyclists, is a critical component of driverless cars’ scene understanding. Although being largely quiet on the self-driving efforts, Apple research releases an archive on LiDAR-only detection of 3D objects on 2017/11/17.

Voxel feature netowrk. The large body of point clouds is first divided into regular voxels and then each non-empty voxel is described by a compact feature vector by proposed feature network. As shown in Figure 2, the feature network is a bit similar to PointNet. The input of each point is a 6-dimensional vector \(\mathbf{v} = [x, y, z, x-c_x, y-c_y, z-c_z]\) where \([c_x, c_y, c_z]^T\) is the centroid of points in this voxel. Then a stack of voxel feature encoding (VFE) layers produce point-wise descriptors for points and voxel-wise descriptors for voxels. The voxel-wise descriptor is essentially element-wise maximum of point-wise descriptors residing in the voxel. (We refer the reader to the paper for details.)

Region Proposal Network. The voxel grids and generated voxel-wise descriptors form regular feature map for objection detection. Region proposal network (RPN), formerly used in 2D cases, is trimmed here to predict 3D bounding boxes and their probability scores.

3. PointNet++: Deep Hierarchical Feature Learning on Point Sets in a Metric Space

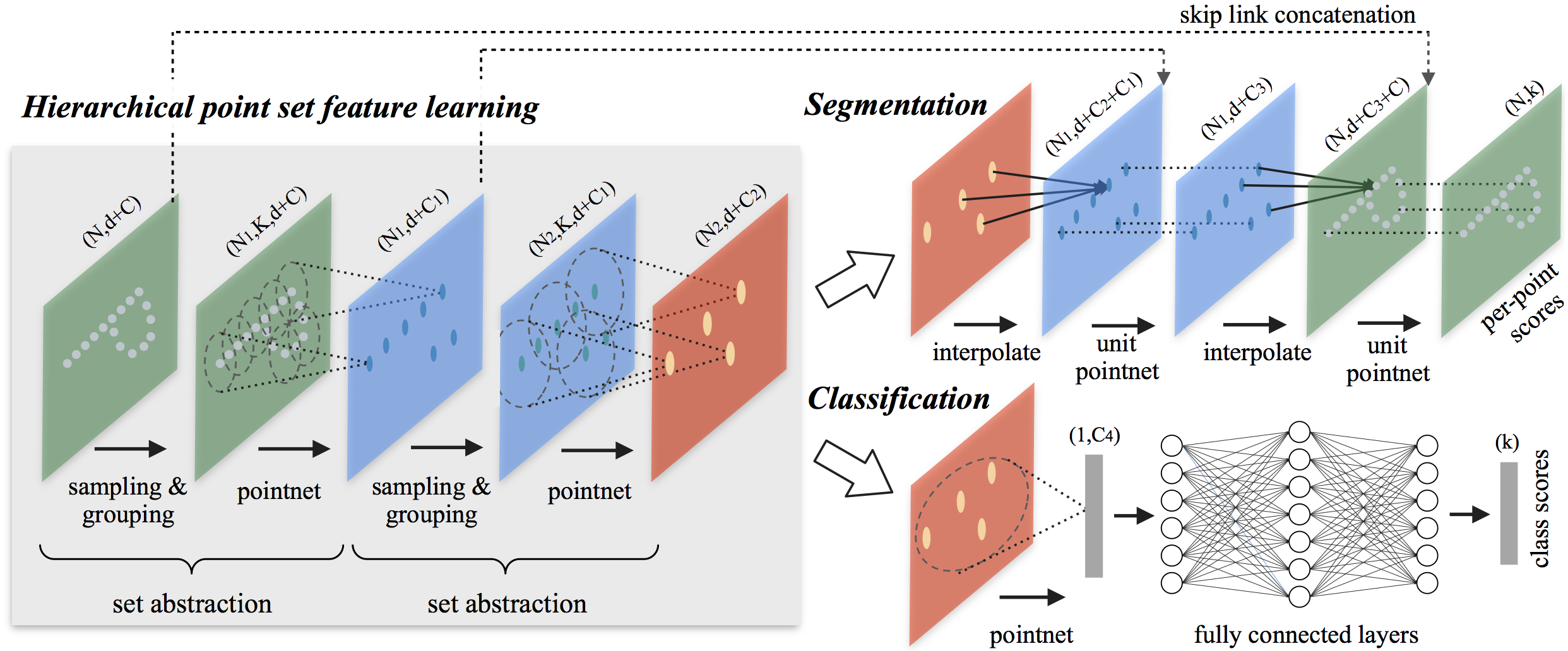
As pointed out by VoxelNet, PointNet lacks generalization to large-scale point set data. It is manipulated on independent points and is consequently blind to local structures of point sets. PointNet++, an extension of PointNet, is proposed to capture local structural information in a hierachical manner.

Set Abstraction. The core of PointNet++ is called set abstraction. It subsamples point set by fathest point sampling (greedily sample the most distant point from other points). Then it encodes each sampled point wih PointNet that considers the points inside the spherical neighborhood of the point (termed group in this paper). Again, the sampled points with encoded features are seen as a new point set input of set abstration layer. Finally, the recursively-sampled point set is greatly contracted to be used for classification and segmentation.

For the segmentation task, it is necessary to assign a label to each point in original point set rather than the sampled points. To this end, an interpolation strategy is used to restore descriptors for eliminated points as weighted sum of neighboring sampled points in the reverse direction of sampling.