SLAM Related
Pose Graph
Constraints of graph-based SLAM can be concluded as two types:
- Sequential constraints introduced by odometry.
- Non-sequential constraints from place recognition (or say loop closure).
Loop closure
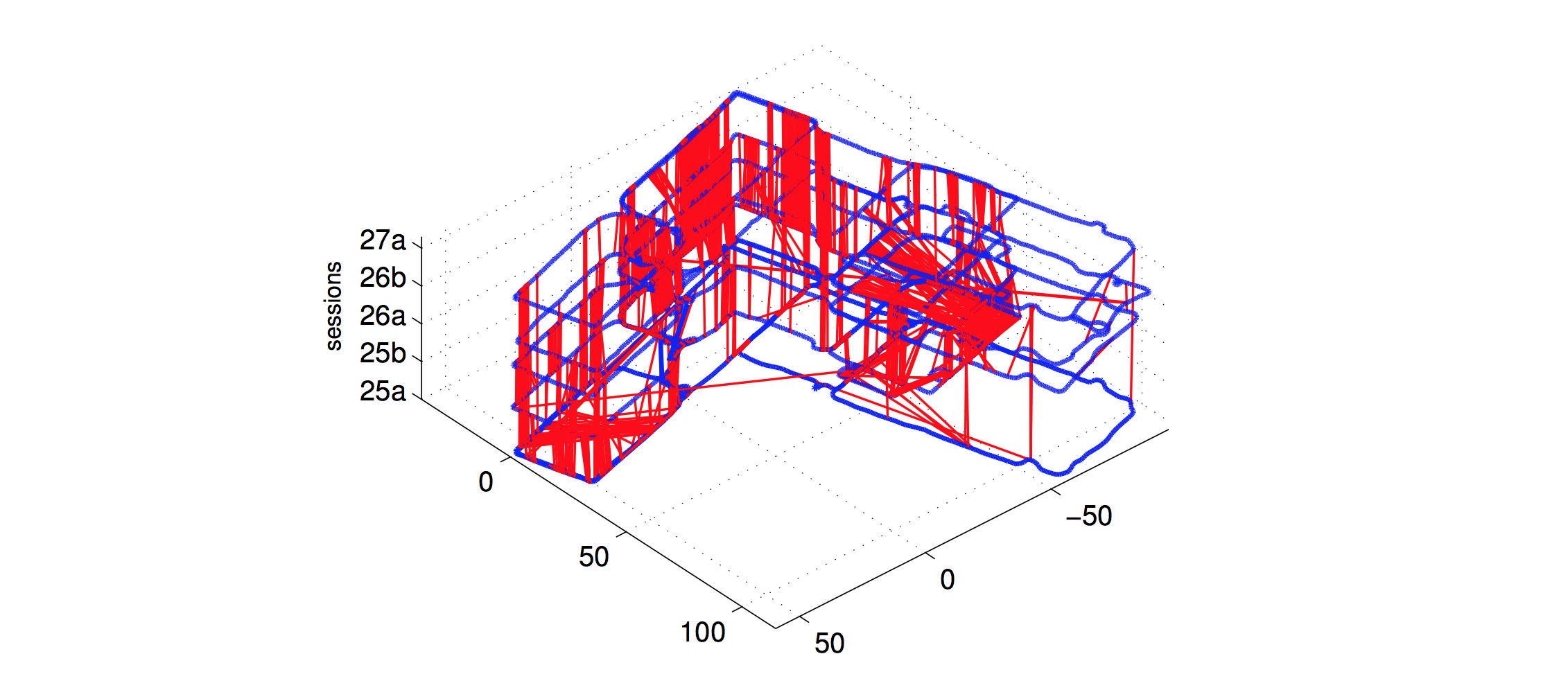
Loop closure equips mobile robots with the capability of recognizing revisted places and re-estimating the map of environments during long-term move.
Perceptual aliasing
One challenge posed to loop closure is perceptual aliasing, which means false positive revisits are identified leading to fake loops. Associating two different places incorrectly can severely corrupt map estimate, as shown by the red lines not parallel to z-axis in Fig 1.
Robust Reconstruction of Indoor Scenes This paper identifies suprious loop closures by optimizing a dense surface registration objective augmented by a line process over the loop closure constraints. A single least-squares objective jointly estimates the global configuration of the scene and the validity of each constraint. The objective is defined as
\[E = \sum_i f(\mathbf{T}_i, \mathbf{T}_{i+1}, \mathbf{R}_i) + \sum_{i, j} l_{ij} f(\mathbf{T}_i, \mathbf{T}_j, \mathbf{T}_{ij}) + \mu \sum_{ij} \Psi(l_{ij}),\]where \(\Psi(l_{ij}) = (\sqrt{l_{ij}} - 1)^2\). The first and second two terms are respectively sequential constraints and close-loop constraints as demonstrated in Pose Graph. A line process \(l_{ij} \in [0, 1]\) models the validity of the corresponding loop closure. Function \(f(.)\) models the pairwise alignment error.
Reference
Robust Loop Closing Over time for Pose Graph SLAM