Graph-Based Neural Network
Related Works
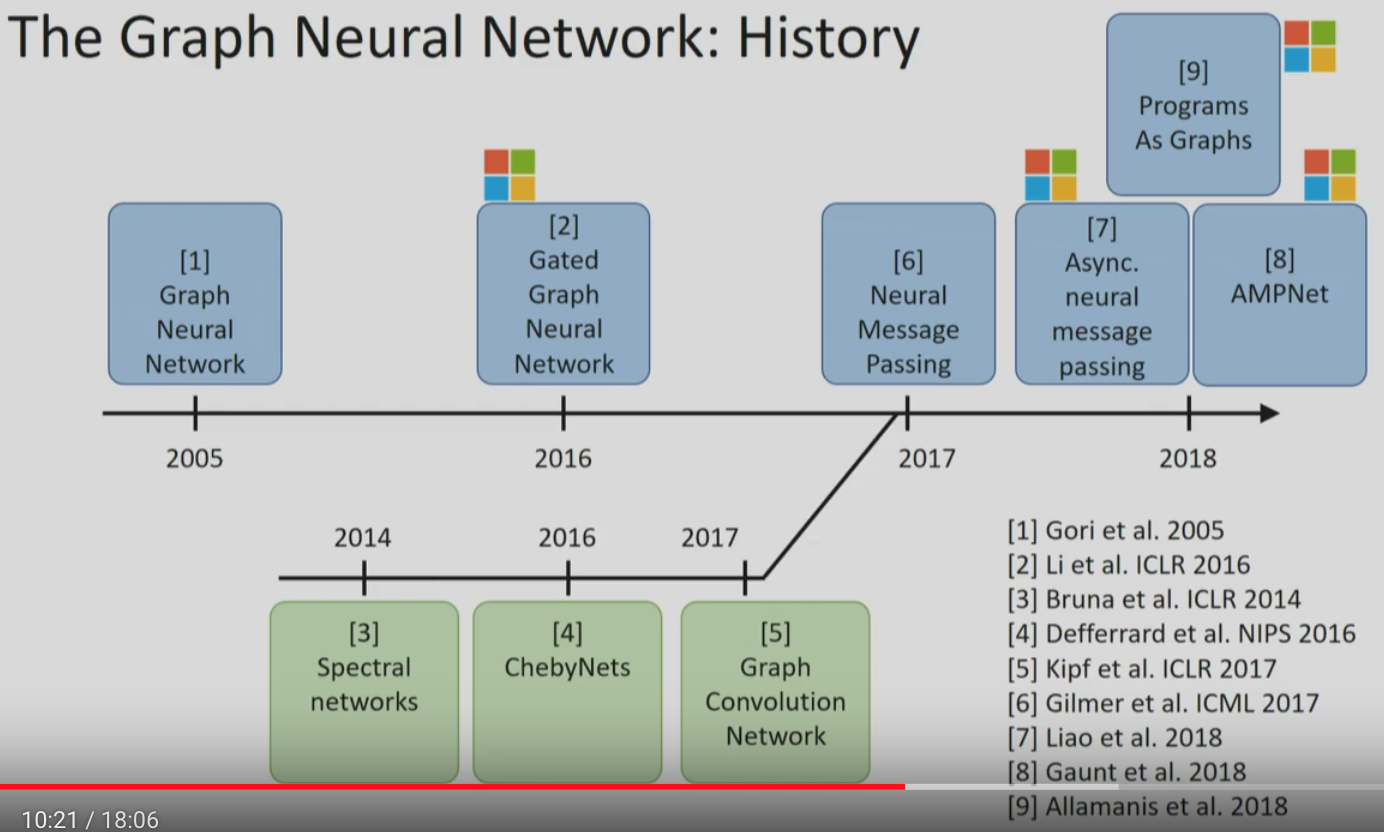
Graph Neural Networks (GNN)
- Person Re-identification with Deep Similarity-Guided Graph Neural Network
- Learning to Find Good Correspondence
Graph Convolutional Networks (GCN)
Graph Convolutional Networks (GCN)
Given \(N\) nodes and their graph structure defined by a symmetric adjacency matrix \(\mathbf{A}\) (binary or weighted), the graph convolutional layer is defined as
\[\mathbf{X}_{i+1} = ReLU (\hat{ \mathbf{A} } \mathbf{X}_i \mathbf{W}_i ).\]\(\mathbf{X}_i \in R^{N \times C_i}\) are the input feature vectors of \(N\) nodes from last layer. \(\mathbf{W}_i \in R^{C_i \times C_{i+1}}\) are the learnable filter parameters of layer \(i+1\). \(\hat{ \mathbf{A} }\) is the re-normalized adjacency matrix defined as
\[\hat{ \mathbf{A} } = \tilde{\mathbf{D}}^{-1/2} \tilde{\mathbf{A}} \tilde{\mathbf{D}}^{-1/2},\]where \(\tilde{\mathbf{A}} = \mathbf{A} + \mathbf{I}\) and \(\tilde{\mathbf{D}}_{ii} = \sum_j \tilde{\mathbf{A}}_{ij}\).
From the perspective of message passing, \(\mathbf{X}_i \mathbf{W}_i\) can be interpreted as the deep message outgoing from the \(N\) nodes and the mulplication with \(\hat{ \mathbf{A} }\) passes (maybe weighted) the messages to neighboring nodes to update the node representations.
Therefore, the GCN can be expressed as a function \(f(\mathbf{X}_0 ,\mathbf{A})\) and \(\hat{ \mathbf{A} }\) can be pre-computed in the preprocess step.