Image Localization

Related works

ICCV2019

Works before ICCV2019

PnP algorithm

“Perspective-n-Point (PnP) is the problem of estimating the pose of a calibrated camera given a set of n 3D points in the world and their corresponding 2D projections in the image.” from wikipedia

P3P

P3P is the PnP problem in its minimal form. Let P be the camera center, and \(A\), \(B\), \(C\) be the 3D points in world frame. Let \(\|PA\|=X\), \(\|PB\|=Y\), \(\|PC\|=Z\), \(\alpha=\angle BPC\), \(\beta=\angle APC\), \(\gamma=\angle APB\), \(p=2cos\alpha\), \(q=2cos\beta\), \(r=2cos\gamma\), \(\|AB\| = c'\), \(\|BC\| = a'\), \(\|AC\| = b'\), as illustrated in Figure 1.

P3P

Figure1. The P3P problem

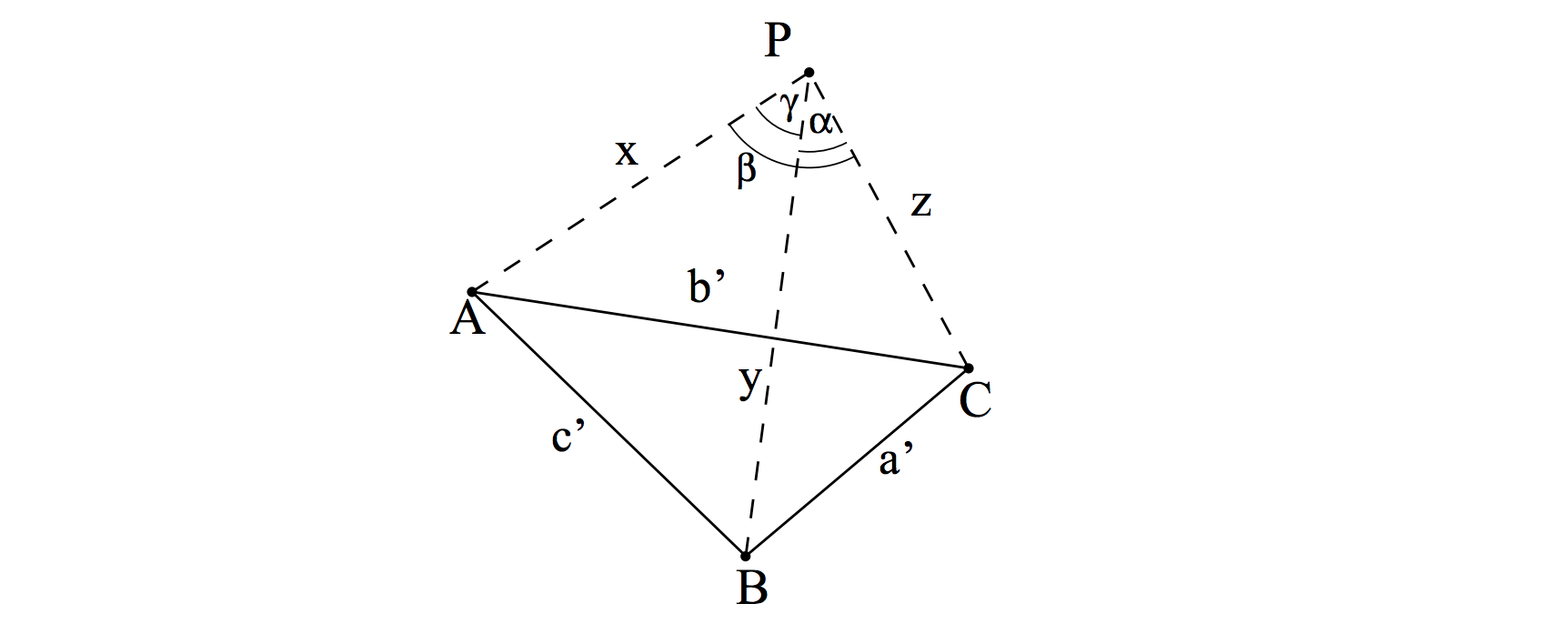
Then the P3P equation system is derived based on the law of cosines (余弦定理):

\[\begin{cases} Y^2 + Z^2 - YZp - a'^2 = 0 \\ Z^2 + X^2 - XZq - b'^2 = 0 \\ X^2 + Y^2 - YXr - c'^2 = 0, \end{cases}\]

where \(X\), \(Y\), \(Z\) are variables to be determined.

To simply the equation system, we let \(X= xZ\), \(Y = yZ\), \(c'= \sqrt{v}Z\), \(a'=\sqrt{av}Z\), \(b'=\sqrt{bv}Z\), then the equation system is turned into

\[\begin{cases} y^2 + 1 - py - av = 0 \\ x^2 + 1 - qx -bv = 0 \\ x^2 + y^2 - xyr - v = 0, \end{cases}\]

where \(x\), \(y\), \(v\) are variables to be determined.

Eliminating \(v = x^2 + y^2 - xyr\), we have

\[\begin{cases} ax^2 + (a-1)y^2 - ar xy + py =1 \\ (b-1)x^2 + b y^2 - brxy + qx = 1. \end{cases}\]

Essentially, the two quatratic equations define two conics, which may have infinite or at most four intersections. Therefore, the P3P problem has either an infinite number of solutions or at most four physical solutions.

P4P, P5P, PnP

Using more than 3 points provides redundant data for the solution of pose estimation. The linear algorithm is generally used [1]. The \(n\) points can form \(\frac{n(n-1)}{2}\) triangles and thus derive \(\frac{n(n-1)}{2}\) second degree polynomial equations based on 余弦定理. By eliminating the set of variables into a single one, we still have \(\frac{n(n-1)}{2} - (n-1) = \frac{(n-1)(n-2)}{2}\) fourth degree polynomial equations. When n = 5, we have the homogeneous equation system:

P5P

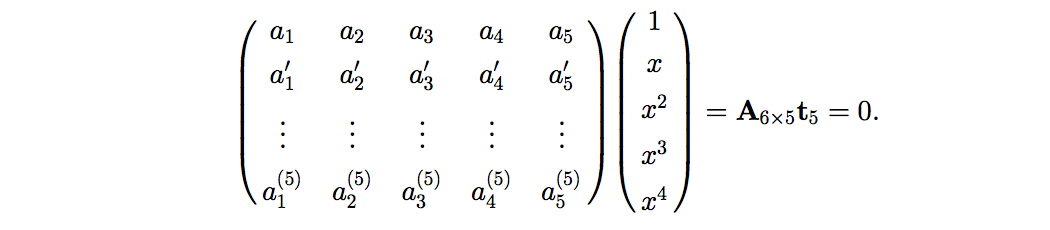
The overdermined equation system can be easily solved by SVD decomposition, where \(t_5\) equals to the right singular vector corresponding to the smallest singular value. The solution can be generalized to cases when \(n>5\).

When \(n=4\), things are a little bit more complicated since the equation system above is underdetermined. We refer the readers to [1] for details.

EPnP

EPnP algorithm is one of the most efficient PnP algorithm which has O(n) complexity. It is composed of three steps:

Step 1. In world coordinate system, find four control points: \(c_j^w (j = 1,...,4)\). One of them is the centroid of the 3D points and the other three are vectors aligned with principle directions of the 3D point set. Then all the 3D points are represented by the barycentric coordinates as a linear combination of the four control points: \(p_i^w = \sum_{j=1}^4 \alpha_{ij} c_j^w (i=1,...,n)\).

Step 2. In camera coordinate system, the equations between 3D points and control points still preserve: \(p_i^c = \sum_{j=1}^4 \alpha_{ij} c_j^c\). Given the 2D projections of the 3D points \(\{p_i\}i=1,...,n\), we have \(\omega_i \begin{bmatrix} u_i \\v_i \\ 1 \end{bmatrix} = K p_i^c = K \sum_{j=1}^4 \alpha_{ij} c_j^c\). Here, \(\omega_i\) and \(\{c_j^c\}j=1,...,4\) are unknowns. By filling in the camera intrinsic matrix, the equation can be expressed as follow:

\[\omega_i \begin{bmatrix} u_i \\ v_i \\ 1 \end{bmatrix} = \begin{bmatrix} f_u & 0 & u_c \\ 0 & f_v & v_c \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} \sum_{j=1}^4 \alpha_{ij} x_j^c \\ \sum_{j=1}^4 \alpha_{ij} y_j^c \\ \sum_{j=1}^4 \alpha_{ij} z_j^c \end{bmatrix}.\]

By eliminating \(\omega_i = \sum_{j=1}^4 \alpha_{ij}z_j^c\), we get two linear equations:

\[\begin{cases} \sum_{j=1}^4 \big( \alpha_{ij}f_u x_j^c + \alpha_{ij} (u_c - u_i) z_j^c \big) = 0 \\ \sum_{j=1}^4 \big( \alpha_{ij}f_v y_j^c + \alpha_{ij} (v_c - v_i) z_j^c \big) = 0 \end{cases}.\]

Therefore, each 3D-2D correspondence yields two linear equations with respect to a 12-vector \(x=[x_1^c, y_1^c, z_1^c, ..., x_4^c, y_4^c, z_4^c]^T\). If consider all the correspondences, we generate a linear system of the form

\[Mx = 0.\]

If we have normalized the coordinates of image pixels to \([u_i, v_i]^T\), the equation system becomes

\[\begin{bmatrix} \alpha_{i1} & \alpha_{i2} & \alpha_{i3} & \alpha_{i4} & 0 & 0 & 0 & 0 & -u_i \alpha_{i1} & -u_i \alpha_{i2} & -u_i \alpha_{i3} & -u_i \alpha_{i4} \\ 0 & 0 & 0 & 0 & \alpha_{i1} & \alpha_{i2} & \alpha_{i3} & \alpha_{i4} & -v_i \alpha_{i1} & -v_i \alpha_{i2} & -v_i \alpha_{i3} & -v_i \alpha_{i4} \end{bmatrix} \begin{bmatrix} x_1^c \\ x_2^c \\ x_3^c \\ x_4^c \\ y_1^c \\ y_2^c \\ y_3^c \\ y_4^c \\ z_1^c \\ z_2^c \\ z_3^c \\ z_4^c \end{bmatrix} \\ = \left(\begin{bmatrix} 1 & 0 & -u_i \\ 0 & 1 & -v_i \end{bmatrix} \otimes \mathbf{\alpha}_i^T \right) \mathbf{x} = \mathbf{0},\]

where \(\otimes\) denotes Kronecker product.

Step 3. The solution of the linear equation system lies in the null space or kernel of \(M^TM\) and can be expressed as \(x = \sum_{i=1}^N \beta_i v_i\), where \(v_i\) are the right-singular vectors of \(M\) corresponding to the zero singular values. Now the unknowns become \(\{\beta_i\}i=1,...,N\). Based on the analysis in [2], the dimension \(N\) of null-space of \(M^TM\) varies from 1 to 4. The algorithm then considers all the four cases and choose the best set of \(\{\beta_i\}i=1,...,N\) with the miminum reprojection error.

Other PnPs and insights

Scene COordinate REgression Network (SCORE-Net)

Network architecture

Reference

[1] Linear N-Point Camera Pose Determination

[2] EPnP: An Accurate O(n)Solution to the PnP Problem

♥ I appreciate your feedback! ♥
· Home ·
© 2024 Lei ZHOU