What Is Bilateral Filter?
Bilateral filter is a smooth filter that smooth edges whilst preserve sharp edges. It is defined as
\[I^{filtered}(x) = \frac{1}{W_p} \sum\limits_{x_i \in \Omega} I(x_i) f_r(||I(x_i) - I(x)||) g_s (||x_i - x||),\]where the normalization term
\[W_p = \sum\limits_{x_i\in\Omega}f_r(||I(x_i) - I(x)||) g_s (||x_i - x||).\]\(f_r\) is the range filter and \(g_s\) is the domain (spatial) filter. \(W_p\) ensures that the weights for all the pixels add up to one.
Combined domain and range filtering will be denoted as bilateral filtering. It replaces the pixel value at x with an average of similar and nearby pixel values. In smooth regions, pixel values in a small neighborhood are similar to each other, and the bilateral filter acts essentially as a standard domain filter, averaging away the small, weakly correlated differences between pixel values caused by noise. Consider now a sharp boundary between a dark and a bright region as in Figure 1.
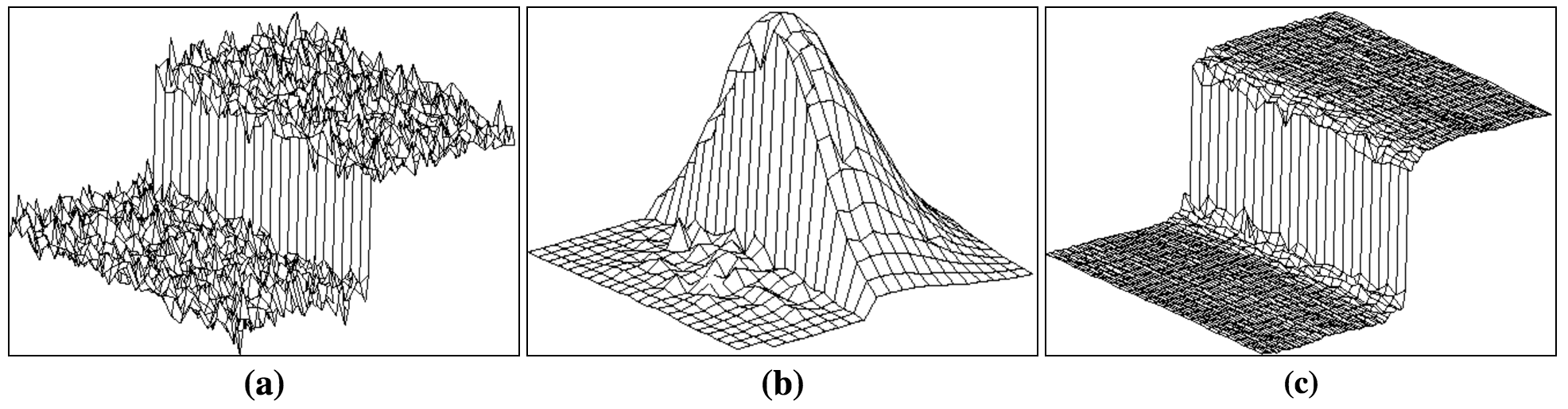
When the bilateral filter is centered, say, on a pixel on the bright side of the boundary, the similarity function s assumes values close to one for pixels on the same side, and values close to zero for pixels on the dark side. The similarity function is shown in Figure 1(b) for a 23x23 filter support centered two pixels to the right of the step in Figure 1(a). As a result, the filter replaces the bright pixel at the center by an average of the bright pixels in its vicinity, and essentially ignores the dark pixels. Conversely, when the filter is centered on a dark pixel, the bright pixels are ignored instead. Thus, as shown in Figure 1(c), good filtering behavior is achieved at the boundaries, thanks to the domain component of the filter, and crisp edges are preserved at the same time, thanks to the range component.