Geometry
- Lie Groups for 2d and 3d Transformation
- Quaternion
- Angle-axis v.s. Quaternion
- Essential & Fundamental Matrix
- PnP
- Bundle Adjustment
- Homography
- “The camera is the measurement of angle.”
- Matrices in CV
- Reference
Lie Groups for 2d and 3d Transformation
A Manifold is an n-Dimensional Topological Space that is locally Euclidean.
A Lie group is a topological group that is also a smooth manifold. Each of them is associated with a Lie algebra which is a vector space. Transformations are required to be composed, inverted, differentiated and interpolated. Lie groups and their associated machinery address all these operations in a pricipled way.
Definition. A nonempty subset \(G \subset \mathbb{R}^{n\times n}\) is called a Lie group if \(g, h \in G \Rightarrow gh \in G\) and \(g \in G \Rightarrow det(g) \neq 0, g^{-1} \in G\).
Mathetical notations
- associative (结合律)- (ab)c=a(bc)
- Abelian (交换律)- abc = cba
SO(3) & so(3)
Elements of the 3D rotation group, SO(3), are represented by 3D rotation matrices. They are all orthogonal matrices with determinant \(+1\). The Lie algebra so(3), associated with SO(3), is the set of \(3\times3\) skew-symmetric or anti-symmetric matrices (i.e., \(A^T=-A\)).
Infinitestimal generators
The key idea introudced by Lie is that any finite transformation can be constructed by the repeated application or integration of infinitestimal (极微小的) transformation. The infinitestimal generators of so(3) correspond to the derivatives of rotation around the each of the standard axes, evaluated at the identity. We take the the rotation by an angle \(\phi\) around x-axes as an example:
\[\mathbf{R}_1(\phi) = \begin{bmatrix} 1 & 0 & 0 \\ 0 & cos\phi & -sin\phi \\ 0 & sin\phi & cos\phi \end{bmatrix} .\]Its derivative w.r.t \(\phi\) evaluated at zero is written into
\[G_1 = \frac{\partial \mathbf{R}_1}{\partial \phi}|_{\phi=0} = \begin{bmatrix} 0 & 0 & 0 \\ 0 & 0 & -1 \\ 0 & 1 & 0 \end{bmatrix}.\]The three infinitestimal generators are derived as:
\[G_1 = \begin{bmatrix} 0 & 0 & 0 \\ 0 & 0 & -1 \\ 0 & 1 & 0 \end{bmatrix}, G_2 = \begin{bmatrix} 0 & 0 & 1 \\ 0 & 0 & 0 \\ -1 & 0 & 0 \end{bmatrix}, G_3 = \begin{bmatrix} 0 & -1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix}\]An element of so(3) is then represented as the linear combination of the three generators:
\[\mathbf{\omega} = [\omega_1, \omega_2, \omega_3]^T \in \mathbb{R}^3\] \[\mathbf{\omega}_{\times} = \omega_1 G_1 + \omega_2 G_2 + \omega_3 G_3 = \begin{bmatrix} 0 & -\omega_3 & \omega_2 \\ \omega_3 & 0 & -\omega_1 \\ -\omega_2 & \omega_1 & 0 \end{bmatrix} \in so(3)\]Since \(G_1\), \(G_2\) and \(G_3\) are derivatives of rotations around three standard axises, \(\omega\) can be considered as the difference of a rotation from the identity.
Exponential & logarithm map
Rodrigues’ formula: a exponential map associates an element of the Lie algebra to a rotation of the Lie group:
\[e^{\omega_{\times}} = I + \frac{sin(|\omega|)}{|\omega|} \omega_{\times} + \frac{1 - cos(|\omega|)}{|\omega|^2} (\omega_{\times})^2\]If \(\omega\) is small, we often take the first-order approximation as \(e^{\omega_{\times}} \approx I + \omega_{\times}\).
A logarithm map associates a rotation of the Lie group with an element of the Lie algebra.
\[\log(R) = \frac{\phi (R - R^T)}{2 sin (\phi)}, \;\; \phi = acos(\frac{trace(R) - 1}{2}).\]Properties
-
If \(\omega_{\times} \in so(3)\), then \(\mathbf{R} = e^{\omega_{\times}} \in SO(3)\). (See proof in [2])
-
As a symmetric matrix, \(\omega_{\times}^3 = -(\omega^T \omega) \cdot \omega_{\times} \triangleq -\theta^2 \omega_{\times}\). Here, \(\theta = \sqrt{\omega_1^2 + \omega_2^2 + \omega_3^2}\). It means the cubic of a skew-symmetric matrix is also a skew-symmetric matrix.
-
The eigenvalues of \(\omega_{\times}\) are \(0, i\theta, -i\theta\) (rank 2).
-
The eigenvalues of \(\mathbf{R} = e^{\omega_{\times}}\) are \(1, e^{i\theta}, e^{-i\theta}\).
-
\(\mathbf{R}\) is a rotation by angle \(\theta\) around an axis. The axis is the engenvector of \(\omega_{\times}\) corresponding to eigenvalue \(0\), i.e., \([\omega_1, \omega_2, \omega_3]^T\).
-
The addition of \(\omega\) corresponds to the multiplication of \(\mathbf{R}\). \(\mathbf{\omega}_{\times} = \omega_1 G_1 + \omega_2 G_2 + \omega_3 G_3\) means the addition of a rotation by \(\omega_1\) around x-axis, a rotation by \(\omega_2\) around y-axis and a rotation by \(\omega_3\) around z-axis.
- \[a_{\times} b = - b_{\times} a\]
SE(3) & se(3)
The group of rigid transformation in 3D space is SE(3). It is represented by a \(4\times4\) matrix:
\[\begin{bmatrix} \mathbf{R} & \mathbf{t} \\ \mathbf{0} & 1 \end{bmatrix}.\]There are six infinitestimal generators of Lie algebra se(3), which correspond to differential translations and rotations:
\[G_1 = \begin{bmatrix} 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\0 & 0 & 0 & 0 \end{bmatrix}, G_2 = \begin{bmatrix} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \\0 & 0 & 0 & 0 \end{bmatrix}, G_3 = \begin{bmatrix} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\0 & 0 & 0 & 0 \end{bmatrix},\] \[G_4 = \begin{bmatrix} 0 & 0 & 0 & 0 \\ 0 & 0 & -1 & 0 \\ 0 & 1 & 0 & 0 \\0 & 0 & 0 & 0 \end{bmatrix}, G_5 = \begin{bmatrix} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 \\ -1 & 0 & 0 & 0 \\0 & 0 & 0 & 0 \end{bmatrix}, G_6 = \begin{bmatrix} 0 & -1 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\0 & 0 & 0 & 0 \end{bmatrix}.\]An element of se(3) is then represented by linear combination of these generators:
\[u_1G_1 + u_2G_2 + u_3 G_3 + \omega_1 G_4 + \omega_2 G_5 + \omega_3 G_6 \in se(3)\]Quaternion
http://people.csail.mit.edu/bkph/papers/Absolute_Orientation.pdf
Angle-axis v.s. Quaternion
| Angle-axis | Quatation | |
|---|---|---|
| Notation | \(\mathbf{x} = \alpha \mathbf{e}\) | \(\mathbf{q} = q_0 + q_1 \mathbf{i} + q_2 \mathbf{j} + q_3 \mathbf{k}\) |
| dimension | 3 | 4, \(| \mathbf{q} | = 1\) |
| angle \(\alpha\) | \(| \mathbf{x} |\) | \(q_r = \cos(\alpha/2)\) |
| \(\mathbf{R}\) | \(\begin{align} & \mathbf{R} = \mathbf{I} + \sin\alpha \mathbf{K}+ (1 - \cos\alpha) \mathbf{K}^2 \\ & \mathbf{K} \textrm{ is cross product matrix of } \mathbf{e} \end{align}\) | See figure below |
| inverse | \(-\mathbf{x} = -\alpha\mathbf{e}\) | \(\begin{align}\mathbf{q}^{-1} &= \mathbf{q}^* \\ &= q_0 - q_1 \mathbf{i} - q_2 \mathbf{j} - q_3 \mathbf{k} \end{align}\) |
| rotate \(\mathbf{p}\) | \(\begin{align} \mathbf{p}' &= \cos\alpha \mathbf{p} + \sin\alpha (\mathbf{e} \times \mathbf{p})\\ &+ (1 - \cos\alpha)(\mathbf{e} \cdot \mathbf{p})\mathbf{e} \end{align}\) | \(\mathbf{p}' = \mathbf{qpq}^{-1}\) (Hamilton product) |
| composition | link | \(\mathbf{q}' = \mathbf{q}_2 \mathbf{q}_1\)(Hamilton product) |
| relationship | \(\mathbf{q} = \cos\frac{\alpha}{2} + \sin\frac{\alpha}{2} (e_1 \mathbf{i} + e_2 \mathbf{j} + e_3 \mathbf{k})\) |
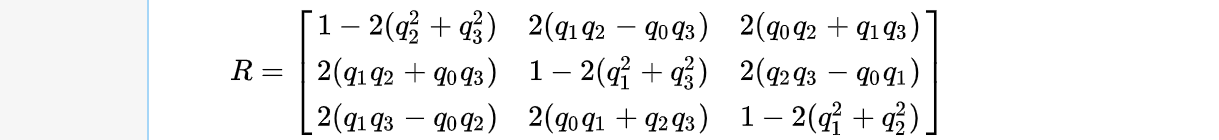
Essential & Fundamental Matrix
Derivation of Essential Matrix
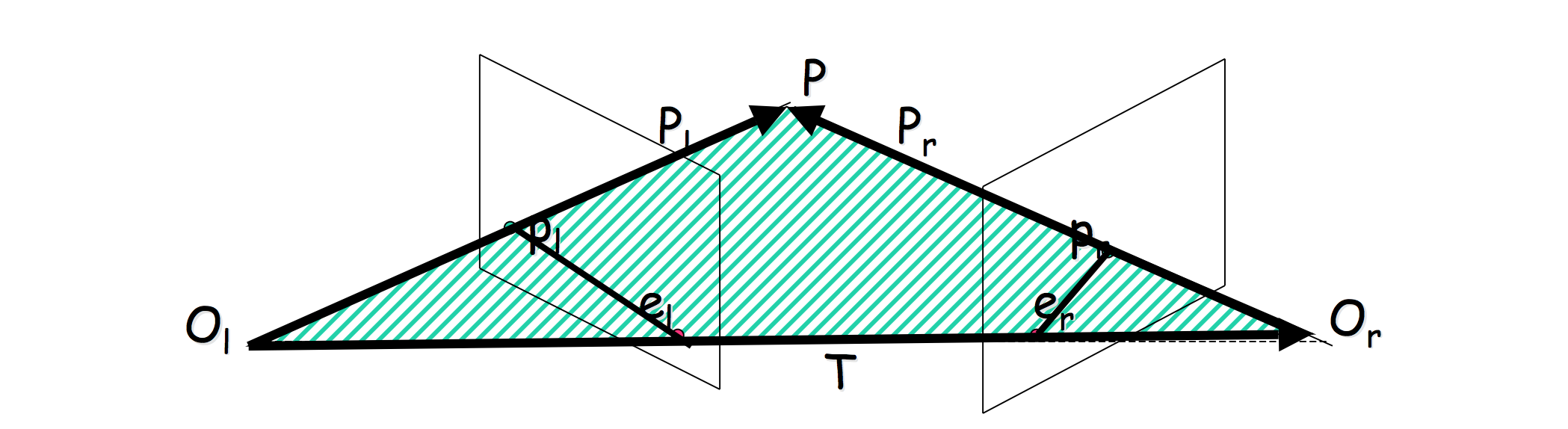
As shown in Figure above, we have two left and right cameras with camera centers \(O_l\) and \(O_r\). \(P\) is a 3D point co-visible in two cameras. We have notations as follows: \(P_l\) is the 3D coordinate of \(P\) in local space of camera \(O_l\) and \(P_r\) is the 3D coordinate of \(P\) in local space of camera \(O_r\). \(T\) is the 3D coordinate of \(O_r\) in local space of camera \(O_l\). The rotation and translation from camera \(O_l\) to camera \(O_r\) are \(R\) and \(t\) respectively. Apparently we have
\[\begin{cases} R P_l + t = P_r \\ R T + t = 0 \end{cases}.\]Thus, we obtain \(t = -RT\) and \(P_r = R(P_l - T)\).
Then, the equation can be derived
\[P_r^T R T_{\times} P_l = 0,\]because \(P_r^T R = (P_l - T)^T\) and \(T_{\times} P_l\) (\(T_{\times}\) is the skew-symmetric matrix) equals to the cross product of vector \(T\) and \(P_l\). Therefore, the two terms are orthogonal to each other. \(R T_{\times}\) is exactly the essential matrix \(E=R T_{\times}\) and \(P_r^T E P_l = 0\). \(P_l\) and \(P_r\) are essentially two viewing rays in local space of two cameras.
The \(R\) and \(T\) have six degrees of freedom. The essential matrix has five degree of freedom by eliminating the common scaling.
Derivation of Fundamental Matrix
Rather than using the camera coordinates, the equation above can be extended to image coordinates, because
\[\begin{cases} p_l = K_l P_l \\ p_r = K_r P_r \end{cases},\]where \(p_l\) and \(p_r\) use homogeneous coordinates and \(K_l\) and \(K_r\) are intrinsics of left and right cameras. Then the equation \(P_r^T E P_l = 0\) can be written into
\[p_r^T K_r^{-T} E K_l^{-1} p_l = p_r^T F p_l = 0.\]\(F = K_r^{-T} E K_l^{-1}\) is called the fundamental matrix.
The fundamental matrix has rank 2. Since all the epipolar lines go through the epipole, e.g. in the left image \(e_l\), we have \(Fe_l = 0\). Hence \(F\) has a null space which is not just the zero vector. So \(F\) is rank 2.
The \(3 \times 3\) homogeneous fundamental matrix has seven degrees of freedom. The common scaling removes one degree and the constraint \(det F = 0\) (rank=2) removes another one.
PnP
Bundle Adjustment
Definition of bundle adjustment
Homography
For any choice of intrinsic parameters, any homography can be realized between two views by some positioning of the two views and a plane.
“The camera is the measurement of angle.”
Matrices in CV
| DoF | |
|---|---|
| Projection matrix | 11 |
| Fundamental matrix | 7 |
| Essential matrix | 5 |
| Homograpy matrix | 8 |
| Affine transform (2d) | 6 |
| Affine transform (Nd) | (N+1)*N |
| Similarity transform (2d) | 4 |
| Similarity transform (3d) | 7 |
Reference
[1] http://ethaneade.com/lie.pdf
[2] Mathetical elucidation of SO(3) and so(3)
[3] http://www.cmth.ph.ic.ac.uk/people/d.vvedensky/groups/Chapter7.pdf
[4] Essential and Fundamental Matrices
[5] Lie Groups for Computer Vision, Ethan Eade
[6] Derivative of the Exponential Map, Ethan Eade