Branch and Bound
Related works
Go-ICP: A Globally Optimal Solution to 3D ICP Point-Set Registration
Introduction
Branch and bound is the most commonly used tool for solving NP-hard optimization problems.
\(f: \mathcal{R}^m \rightarrow \mathcal{R}\) is the objective function defined over an m-dimensional domain \(\mathcal{Q}_{init}\). We aim to find the global optimal value \(f^* = inf_{x \in \mathcal{Q}_{init}} f(x) = \Phi_{min}(\mathcal{Q}_{init})\).
For any subspace \(\mathcal{Q} \in \mathcal{Q}_{init}\), we use lower and upper bound functions \(\Phi_{lb}\) and \(\Phi_{ub}\) that satisfy
\[\Phi_{lb}(\mathcal{Q}) < \Phi_{min}(\mathcal{Q}) < \Phi_{ub}(\mathcal{Q}).\]Then, the Branch and Bound algorithm takes steps as follows:
-
partition \(\mathcal{Q}_{init}\) into e.g. two subspaces \(\mathcal{Q}_{init} = \mathcal{Q}_1 \cup \mathcal{Q}_2\)
-
compute lower and upper bound for each subspace: \(\Phi_{lb}(\mathcal{Q}_i)\) and \(\Phi_{ub}(\mathcal{Q}_i)\) , \(i=1,2\). The upper bound is actually the value at one feasible point.
- update the global lower and upper bounds on \(f^*\) and terminate if lower and upper bounds are close enough.
- \(L = \min\{\Phi_{lb}(\mathcal{Q}_1), \Phi_{lb}(\mathcal{Q}_2) \}\),
- \(U = \min\{\Phi_{ub}(\mathcal{Q}_1), \Phi_{ub}(\mathcal{Q}_2) \}\),
- terminate if \(U - L \leq \epsilon\).
- partition \(\mathcal{Q}_1\) and \(\mathcal{Q}_2\), and repeat 2 and 3. (The number of subspaces grows exponentially.)
Example
In this section, we use the Go-ICP algorithm as an example. It is a globally-optimal solution to point set registration based on Branch and Bound algorithm.
Branch of SE(3)
The domain of 3D motions (the SE(3) group) is minimally parameterized by axis-angle \(\mathbf{r} \in [-\pi, \pi]^3\) (the minimum cude that enclosing the \(\pi\)-ball) for rotation and \(\mathbf{t} \in [-\xi, \xi]^3\) for translation. During BnB search, each of the rotation cube and translation cube is subdivided into eight smaller cubes using the octree data structure. Illustration shown below.
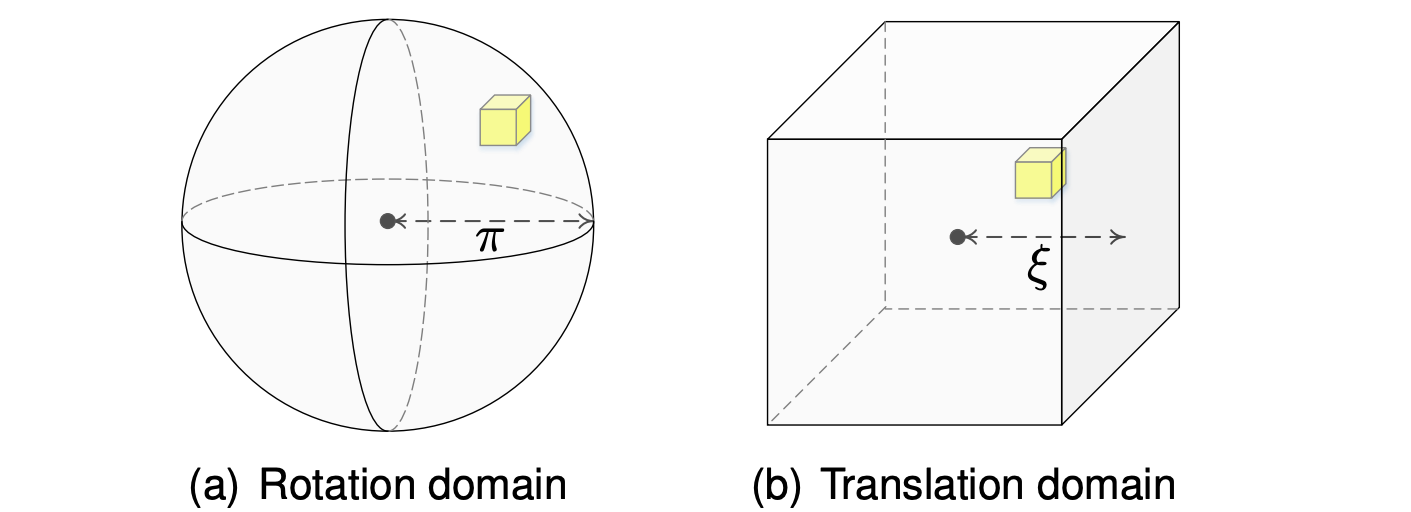
Rather than search inside a 6-D space, GO-ICP uses a nested BnB search. The outer BnB searches the rotation space and solves the bounds and corresponding optimal translations by calling an inner translation BnB. In this way, it only needs to maintain two queues with significantly fewer cubes.
Bound of registration error
Given a sub-domain of rotation and translation \(C_r \times C_t\), we aim to compute the bound of registration error between two point sets, i.e.,
\[E(R, t) = \sum_{i=1}^N e_i(R, t) =\sum_{i=1}^N \|R x_i + t - y_i \|,\]where \((x_i, y_i)\) is a pair of correspondence found by nearest neighbor search. To identify the error bound of each pair, we need to first determine the bound of transformed point \(R x_i + t\).
Given a rotation cube \(C_r\) of half side-length \(\sigma_r\) with angle-axis \(r_0\) as the center, for any angle-axis \(r \in C_r\), the distance from \(R_r x\) to \(R_{r_0} x\) can be proved to be bounded by
\[\| R_r x - R_{r_0} x \| \leq 2sin(\min( \sqrt{3} \sigma_r / 2, \pi/2)) \|x \| = \gamma_r.\]Similarly, given a translation cube \(C_t\) with half side-length \(\sigma_t\) centered at \(t_0\), for any \(t \in C_t\), the distance is bounded by
\[\|(x-t) - (x-t_0) \| \leq \sqrt{3} \sigma_t = \gamma_t.\]Illustration shown below.
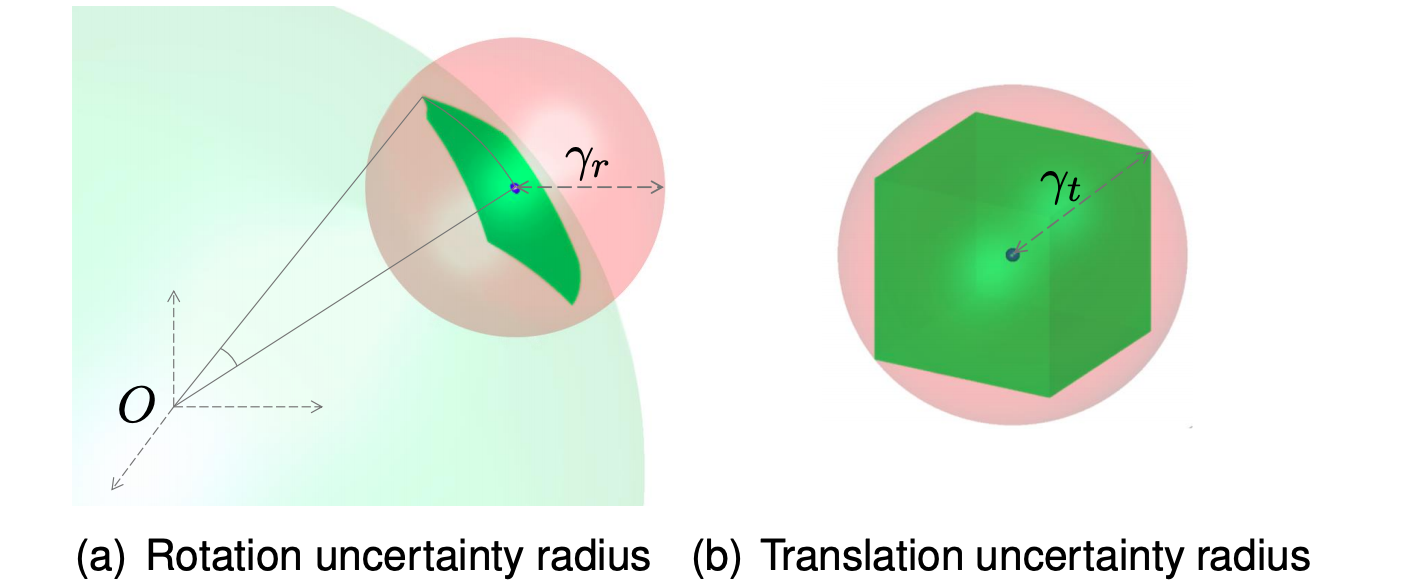
The upper bound of L2 error for a pair \((x_i, y_i)\) is above bounded by \(e_i(R_0, t_0)\), since it cannot be less than the minimal error. The lower bound is derived as
\[\begin{split} e_i(R, t) &= \|R x_i + t - y_i \| \\ &= \|(R_0 x_i + t_0 - y_i) + (Rx_i - R_0 x_i) + (t - t_0)\| \\ &\geq \|(R_0 x_i + t_0 - y_i) \| - (\| Rx_i - R_0 x_i \| + \|t - t_0 \|) \\ &\geq \|(R_0 x_i + t_0 - y_i) \| - (\gamma_r + \gamma_t)\\ &= e_i(R_0, t_0) - (\gamma_r + \gamma_t) \end{split}\]Algorithm
